Elaborado por: Ing. Wilfredo Diaz e Ing. Ricardo Diaz
CONTENIDO
El error se define como la diferencia entre el valor verdadero y el obtenido experimentalmente. Los errores no siguen una ley determinada y su origen está en múltiples causas.
Los errores pueden clasificarse en dos grandes grupos
A) Errores sistemáticos
Son aquéllos que se reproducen constantemente y en el mismo sentido. Afecta a todas las mediciones de un modo definido y es el mismo para todas ellas, Estos errores tienen un signo determinado, Atendiendo a su origen los errores sistemáticos se clasifican en:
El error absoluto no puede ser conocido con exactitud ya que desconocemos el valor exacto de la medida.
Hay que resaltar que el valor de una magnitud debe tener el mismo orden decimal que el error absoluto. Esto es razonable dado que no tendría sentido encontrar el valor de una magnitud con un grado de precisión superior al del error de la medida. Así, no podemos medir décimas de milímetro con una regla cuya sensibilidad es del milímetro.
Finalmente, se acepta como criterio que si el valor de una medida es leído de una tabla u otro lugar, sin indicación de su error, se tomará como error una unidad del orden de la última cifra con que se expresa; por ejemplo, si en una tabla aparece que el valor de una medida es de 0.056 sin ninguna indicación de error, se conviene en que el mismo es de ±0.001. En la siguiente tabla se dan distintos ejemplos.
Caso en el que se realizan varias medidas de una misma magnitud. Con el fin de alcanzar cierta validez estadística en los resultados de las medidas, es muy conveniente repetir varias veces la determinación del valor de la magnitud problema. Los resultados de las medidas individuales pueden presentarse poco o muy dispersas, en función de esta dispersión será conveniente aumentar o no, el número de determinaciones del valor de la magnitud.
Para decidir el número determinaciones del valor de una magnitud física que deseamos medir seguiremos el siguiente procedimiento.
Se realizan siempre tres medidas de la magnitud, se calcula el valor medio de estas tres medidas, dado por:
Una vez realizadas las medidas necesarias se toma como valor verdadero de la magnitud, el valor medio de la misma calculado sobre el número total de medidas realizadas. En cuanto al correspondiente error se determina según los casos como sigue:
que proporciona el error cuadrático medio o desviación estándar de las medidas, donde xi son cada uno de los valores medidos, xN es la media aritmética de las medidas individuales y N es el número de medidas realizadas.
La medida indirecta de una magnitud se alcanza por aplicación de una fórmula a un conjunto de medidas directas, (variables independientes o datos), que las relacionan con la magnitud problema.
Si en dicha fórmula aparecen números irracionales tales como pi, e, etc., se debe elegir el número de cifras significativas con que deben tomarse a la hora de realizar los cálculos correspondientes, de modo que los errores cometidos al aproximar estos números irracionales no afecten a la magnitud del error absoluto de la magnitud que queremos determinar. Supongamos que la magnitud F es función de otras magnitudes físicas, estando relacionada con ellas por F = f ( x, y, z, ...). Supongamos además, que se han realizado medidas de las citadas variables, x, y, z...; y se han determinado su valor y su error. Para realizar el cálculo del error absoluto de F, en función de los errores absolutos cometidos en las determinaciones directas de x, y, z... se procederá de la siguiente forma: En primer lugar se obtiene la diferencial total de F en función de las diferenciales de las variables x, y, z, ...; mediante :
A continuación asimilamos las diferentes diferenciales a los errores absolutos, y además consideramos que en el cálculo del error de F debemos ponernos en el caso más desfavorable, es decir, error mayor, para lo cual tomaremos los valores absolutos de las derivadas parciales, con el fin de tener una suma de términos positivos, obteniendo para el valor del error absoluto de F el resultado:
En este problema se presenta una notable simplificación en el caso en el que la función considerada sea de la forma:
con a, b, c, ... constantes positivas o negativas, ya que en este caso, podemos proceder del siguiente modo, tomando logaritmos neperianos:
si a continuación obtenemos la diferencial:
teniendo en cuenta la diferencial logarítmica dada por:
|tenemos que:
donde asimilando de nuevo los diferenciales totales a los errores absolutos obtenemos:
PRECISIÓN, EXACTITUD Y SENSIBILIDAD
En lo que respecta a los aparatos de medida, hay tres conceptos a definir exactitud, precisión, y sensibilidad.
La exactitud se define como el grado de concordancia entre el valor verdadero y el experimental. De modo que, un aparato es exacto si las medidas realizadas con él son todas muy próximas al valor "verdadero" de la magnitud medida.
La precisión hace referencia a la concordancia entre una medida y otras de la misma magnitud, realizadas en condiciones sensiblemente iguales. De modo que, un aparato será preciso cuando la diferencia entre diferentes medidas de una misma magnitud sea muy pequeña.
La exactitud implica normalmente precisión, pero la afirmación inversa no es cierta, ya que pueden existir aparatos muy precisos que posean poca exactitud debido a los errores sistemáticos. En general, se puede decir que es más fácil conocer la precisión de un aparato que su exactitud.
La sensibilidad de un aparato está relacionada con el valor mínimo de la magnitud que es capaz de medir. Normalmente, se admite que la sensibilidad de un aparato viene indicada por el valor de la división más pequeña de la escala de medida. En muchas ocasiones, de un modo erróneo, se toman como idénticos los conceptos de precisión y sensibilidad.
Decimos que una medida es tanto más exacta cuanto más pequeños sean los errores sistemáticos. La medida será más precisa cuanto más pequeños sean los errores accidentales.
y varía entre 0 (no existe correlación) y ±1 (correlación completa). Las expresiones correspondientes al cálculo del error de la pendiente y la ordenada en el origen son:
2) ¿Cómo se clasifican los errores?
Los errores pueden clasificarse en dos grandes grupos
Ejercicios Propuestos
CONTENIDO
INTRODUCCIÓN
Todas las medidas experimentales vienen afectadas de una cierta imprecisión inevitable debida a las imperfecciones del aparato de medida, o a las limitaciones impuestas por nuestros sentidos que deben registrar la información. El principal objetivo de la teoría de errores consiste en acotar el valor de dichas imprecisiones, Dado que el valor de las magnitudes físicas se obtiene experimentalmente por medida.El error se define como la diferencia entre el valor verdadero y el obtenido experimentalmente. Los errores no siguen una ley determinada y su origen está en múltiples causas.
CLASIFICACIÓN DE ERRORES
Los errores pueden clasificarse en dos grandes grupos
A) Errores sistemáticos
Son aquéllos que se reproducen constantemente y en el mismo sentido. Afecta a todas las mediciones de un modo definido y es el mismo para todas ellas, Estos errores tienen un signo determinado, Atendiendo a su origen los errores sistemáticos se clasifican en:
- Errores teóricos. Son los introducidos por la existencia de condiciones distintas a las idealmente supuestas para la realización del experimento.
- Errores instrumentales. Son los inherentes al propio sistema de medida, debido a aparatos mal calibrados, mal reglados o, simplemente, a las propias limitaciones del instrumento o algún defecto en su construcción. Estos errores pueden ser atenuados por comparación con otros aparatos "garantizados", cuyo error instrumental sea más "pequeño" y controlable.
- Errores personales. Son los debidos a las peculiaridades del observador que puede, sistemáticamente, responder a una señal demasiado pronto o demasiado tarde, estimar una cantidad siempre por defecto, etc.
- Error de la elección del método Corresponde a una elección inadecuada del método de medida de la magnitud. Este tipo de error puede ponerse de manifiesto cambiando el aparato de medida, el observador, o el método de medida.
B) Errores accidentales
Se denominan errores accidentales a aquellos que se producen en las pequeñas variaciones que aparecen entre observaciones sucesivas realizadas por un mismo operador. Las variaciones no son reproducibles de una medición a otra, y no presentan más que por azar la misma magnitud en dos mediciones cualesquiera del grupo. Las causas de estos errores son incontrolables para un observador. Los errores accidentales son en su mayoría de magnitud muy pequeña y para un gran número de mediciones se obtienen tantas desviaciones positivas como negativas. Para tratar adecuadamente este tipo de errores es preciso hacer uso de la estadística y hablar en términos probabilísticos. Como veremos, no podemos decir que el error de una medida sea de 5 unidades, por ejemplo, sino que habrá que decir que existe una probabilidad P (del 75%, por ejemplo) de que el error.
Desde el punto de vista de su cuantificación, los errores se clasifican en:
A) Error absoluto
Se define como la diferencia que existe entre el valor real de la magnitud a medir y el obtenido en una medida. Puesto que es una diferencia de valores de una misma magnitud, el error absoluto se expresa en las mismas unidades que la magnitud. Así pues, si x es el valor medido, x* el valor real y ∆x el error instrumental o sensibilidad del aparato de medida, se satisface la relación
que se representa en la forma:
El error absoluto, que se identifica en primera aproximación con el error instrumental, es el parámetro básico utilizado en la descripción de una medida y es, en general, conocido o determinable a priori. Sin embargo, no es el que define con mayor efectividad la aproximación de la medida.
El error absoluto no puede ser conocido con exactitud ya que desconocemos el valor exacto de la medida.
B) Error relativo
Error relativo Se define como el cociente entre el error absoluto ∆x y el valor real x* de la magnitud
donde x es el valor medido.
Utilizaremos la segunda expresión cuando, como es habitual, no conozcamos el valor real de la magnitud. Es costumbre expresar el error relativo porcentualmente,
EXPRESIÓN DEL ERROR
Presentar una medida experimental significa dar el valor de dicha cantidad y expresar cual es su error; no tiene sentido establecer un determinado valor si no se acota debidamente el mismo. Así, la expresión correcta de una medida debe ser: x ± ∆x Dado el significado de cota de imprecisión que tiene el error absoluto, éste siempre se expresa con una única cifra significativa, es decir, con el primer dígito comenzando por la izquierda distinto de cero; este número ser redondeado por exceso en una unidad si la segunda cifra significativa es 5 o mayor de 5.
Este convenio de expresión del error encuentra dos excepciones: que la primera cifra significativa sea un 1 o que siendo la primera un 2, la segunda no llega 5; en estos casos, el error vendrá dado por las dos primeras cifras significativas.
Hay que resaltar que el valor de una magnitud debe tener el mismo orden decimal que el error absoluto. Esto es razonable dado que no tendría sentido encontrar el valor de una magnitud con un grado de precisión superior al del error de la medida. Así, no podemos medir décimas de milímetro con una regla cuya sensibilidad es del milímetro.
Finalmente, se acepta como criterio que si el valor de una medida es leído de una tabla u otro lugar, sin indicación de su error, se tomará como error una unidad del orden de la última cifra con que se expresa; por ejemplo, si en una tabla aparece que el valor de una medida es de 0.056 sin ninguna indicación de error, se conviene en que el mismo es de ±0.001. En la siguiente tabla se dan distintos ejemplos.
DETERMINACIÓN DE LOS ERRORES COMETIDOS EN LAS MEDIDAS DIRECTAS
Cuando realicemos la medida de cualquier magnitud deberemos indicar siempre una estimación del error asociado a la misma. Dado que no conocemos el valor "verdadero" de la magnitud que deseamos medir, se siguen ciertos procedimientos para hacer una estimación tanto del valor "verdadero" de la magnitud, como de una cota de error, que nos indique la incertidumbre en la determinación realizada. Distinguiremos dos casos bien diferenciados:
Caso en el que se realiza una única medida de una magnitud. En este caso consideramos que el error absoluto coincide con el valor de la sensibilidad del aparato utilizado para realizar la medida. De este modo el resultado de una medida lo indicaremos en la forma:
Para decidir el número determinaciones del valor de una magnitud física que deseamos medir seguiremos el siguiente procedimiento.
Se realizan siempre tres medidas de la magnitud, se calcula el valor medio de estas tres medidas, dado por:
y se halla la dispersión total D de las mismas, es decir, la diferencia entre los valores extremos de las medidas (valor máximo de las medidas obtenidas menos el valor mínimo) y finalmente se obtiene el tanto por ciento de dispersión, T, que viene dado por:
Si el valor de la dispersión total D no es mayor que el valor de la sensibilidad del aparato de medida, D ≤ S, en este caso se toma como estimación del valor "verdadero" de la magnitud el valor medio de las tres medidas x3 y como error absoluto la sensibilidad. Ahora bien, si el valor de la dispersión total D es mayor que el de la sensibilidad del aparato, D > S, procedemos a aumentar el número de medidas de la magnitud. El criterio a seguir en este aumento viene condicionado por el valor del porcentaje de dispersión T del modo indicado en la siguiente tabla:
Una vez realizadas las medidas necesarias se toma como valor verdadero de la magnitud, el valor medio de la misma calculado sobre el número total de medidas realizadas. En cuanto al correspondiente error se determina según los casos como sigue:
- Si se han realizado tres medidas, se toma como error absoluto el valor de la sensibilidad del aparato, que como hemos indicado anteriormente, es el error absoluto de cada una de las medidas individuales.
- Si se han realizado seis medidas, entonces se calcula el error de dispersión definido como D6/4 (cuarta parte de la dispersión total de las seis medidas, es decir, la diferencia entre la mayor y menor de todas las medidas realizadas), y se asigna como error absoluto de las medidas, el máximo entre este valor y la sensibilidad del aparato.
- Si se han realizado quince medidas o más, el error absoluto puede calcularse por la expresión:
DETERMINACIÓN DEL ERROR DE UNA MAGNITUD MEDIDA INDIRECTAMENTE
La medida indirecta de una magnitud se alcanza por aplicación de una fórmula a un conjunto de medidas directas, (variables independientes o datos), que las relacionan con la magnitud problema.
Si en dicha fórmula aparecen números irracionales tales como pi, e, etc., se debe elegir el número de cifras significativas con que deben tomarse a la hora de realizar los cálculos correspondientes, de modo que los errores cometidos al aproximar estos números irracionales no afecten a la magnitud del error absoluto de la magnitud que queremos determinar. Supongamos que la magnitud F es función de otras magnitudes físicas, estando relacionada con ellas por F = f ( x, y, z, ...). Supongamos además, que se han realizado medidas de las citadas variables, x, y, z...; y se han determinado su valor y su error. Para realizar el cálculo del error absoluto de F, en función de los errores absolutos cometidos en las determinaciones directas de x, y, z... se procederá de la siguiente forma: En primer lugar se obtiene la diferencial total de F en función de las diferenciales de las variables x, y, z, ...; mediante :
En este problema se presenta una notable simplificación en el caso en el que la función considerada sea de la forma:
PRECISIÓN, EXACTITUD Y SENSIBILIDAD
En lo que respecta a los aparatos de medida, hay tres conceptos a definir exactitud, precisión, y sensibilidad.
La exactitud se define como el grado de concordancia entre el valor verdadero y el experimental. De modo que, un aparato es exacto si las medidas realizadas con él son todas muy próximas al valor "verdadero" de la magnitud medida.
La precisión hace referencia a la concordancia entre una medida y otras de la misma magnitud, realizadas en condiciones sensiblemente iguales. De modo que, un aparato será preciso cuando la diferencia entre diferentes medidas de una misma magnitud sea muy pequeña.
La exactitud implica normalmente precisión, pero la afirmación inversa no es cierta, ya que pueden existir aparatos muy precisos que posean poca exactitud debido a los errores sistemáticos. En general, se puede decir que es más fácil conocer la precisión de un aparato que su exactitud.
La sensibilidad de un aparato está relacionada con el valor mínimo de la magnitud que es capaz de medir. Normalmente, se admite que la sensibilidad de un aparato viene indicada por el valor de la división más pequeña de la escala de medida. En muchas ocasiones, de un modo erróneo, se toman como idénticos los conceptos de precisión y sensibilidad.
Decimos que una medida es tanto más exacta cuanto más pequeños sean los errores sistemáticos. La medida será más precisa cuanto más pequeños sean los errores accidentales.
TRATAMIENTO DE LOS DATOS
En muchas ocasiones, los resultados obtenidos de los datos se interpretan mejor con ayuda de una representación gráfica. Además, este procedimiento muestra una tendencia que permite estimar los valores en otros puntos diferentes a los experimentales o demuestra una determinada relación matemática entre las variables representadas. Por ello, conviene exponer varios métodos de ajuste de datos, los cuales son:
A) El Método de Mínimos Cuadrados.
Con frecuencia, se plantea el problema de encontrar una expresión matemática y = f(x) de la ley física que rige el comportamiento de un determinado fenómeno a partir de una serie de N medidas (xi , yi ) de las magnitudes x e y que lo caracterizan. Cuando la representación gráfica del fenómeno estudiado proporciona una distribución de los puntos experimentales en forma prácticamente lineal, es conveniente determinar la ecuación de la recta que será expresión de la ley física que rige el fenómeno estudiado, utilizando para ello el método de mínimos cuadrados. Dicha recta debe cumplir la condición de que los puntos experimentales, queden distribuidos simétricamente a ambas partes de la misma, y además, lo más próximos posible. Esta condición se cumple si se obliga a que la recta de ecuación:
cumpla con que la expresión:
tenga un valor mínimo. Derivando c respecto a "a" y "b", y anulando ambas derivadas, tras una serie de operaciones se obtiene:
Además de los valores de la pendiente y la ordenada en el origen, es interesante obtener el denominado coeficiente de correlación lineal “r”, que nos da una medida del grado de correlación entre los valores de las variables x e y, es decir, hasta qué‚ punto x e y están relacionadas mediante una función lineal. La expresión de “r” es:
B) Interpolación en tablas
La interpolación en tablas permite encontrar valores de las variables dependientes para valores concretos de la variable independiente que no están explícitamente en la tabla.
Así, en una tabla de simple entrada para las magnitudes X e Y, se localizarán los valores entre los que se quiere interpolar, x1 y x2, a los que corresponden y1 e y2. Para un valor dado de x comprendido entre x1 y x2, el valor de y correspondiente viene dado por:
y el error correspondiente es:
En las tablas de doble entrada para cada pareja de valores x, y se proporciona el valor correspondiente a una tercera variable z relacionada con las dos anteriores. Si la tabla responde al tipo:
donde z es el valor buscado y comprendido entre x1 y x2 e y1 e y2, entonces:
y el correspondiente error viene dado por:
C) Teorema de Taylor
El análisis completo de una función puede resultar muy difícil. Una forma de abordar este problema es aproximar la función por una más sencilla. En este caso vamos a aproximar las funciones por polinomios. Dicha aproximación se hace cerca de un valor concreto y solo servirá para valores cercanos. A medida que nos alejemos, la aproximación será menos confiable y es posible que el polinomio se aleje mucho de la función bajo estudio.
Dada f una función con por lo menos n derivadas en a tendremos un único polinomio de grado n tal que las primeras n derivadas de f coinciden con las de P.
El teorema de Taylor es una generalización del teorema del valor medio de Lagrange. Cuando aplicamos el teorema de Taylor usualmente dejamos fijo el punto a y tratamos b como variable. La fórmula de Taylor es más fácil de escribir en esta situación si cambiamos la variable b por la variable Xo que usamos normalmente. Este polinomio es el Polinomio de Taylor de f en Xo de orden n. Mas precisamente, su expresión es
En la expresión, n! es el factorial de n, o sea el producto de todos los números naturales de 1 a n
Expresión del resto de Taylor
El error que se comete al aproximar f por su polinomio de Taylor de orden n en Xo es Rn(x) = f(x) − Pn(x) y lo llamaremos resto de orden n. En general no va a ser posible calcularlo y lo que queremos es encontrar una expresión fácil que permita acotarlo, para saber la magnitud del error cometido al usar la aproximación.
Si f es una función con n +1 derivadas continuas, el resto de su polinomio de Taylor de orden n en Xo es
Es importante recalcar que el punto c que aparece en la expresión anterior depende del punto x con c en el intervalo (Xo; X) si Xo < x y c en el intervalo (x; Xo) si x < Xo.
En general si la (n+1) derivada de f está acotada por una constante M en el intervalo (a,b) que se menciona en el Teorema de Taylor, es decir, si
entonces
Así pues, si al aproximar por un polinomio de grado n, la siguiente derivada está acotada por M>0, entonces podemos estimar de la siguiente manera el error.
PREGUNTAS FRECUENTES
1) ¿Que es el error?
Se define como la diferencia entre el valor verdadero y el obtenido experimentalmente
Se define como la diferencia entre el valor verdadero y el obtenido experimentalmente
2) ¿Cómo se clasifican los errores?
Los errores pueden clasificarse en dos grandes grupos
A) Errores sistemáticos
B) Errores accidentales
3) ¿Que es el error absoluto?
Se define como la diferencia que existe entre el valor real de la magnitud a medir y el obtenido en una medida.
Se define como la diferencia que existe entre el valor real de la magnitud a medir y el obtenido en una medida.
4) ¿Que es el error relativo?
Se define como el cociente entre el error absoluto ∆x y el valor real x * de la magnitud
Se define como el cociente entre el error absoluto ∆x y el valor real x * de la magnitud
5) ¿Cómo se expresa el error?
la expresión correcta de una medida debe ser: x ± ∆x
la expresión correcta de una medida debe ser: x ± ∆x
PRÁCTICAS
1) El siguiente ejemplo sirve para ver de forma práctica las actuaciones descritas hasta aquí. Supongamos que se quiere determinar el volumen de un cilindro; para ello, puesto que este parámetro viene dado por:
1) El siguiente ejemplo sirve para ver de forma práctica las actuaciones descritas hasta aquí. Supongamos que se quiere determinar el volumen de un cilindro; para ello, puesto que este parámetro viene dado por:
Se procede a calcular el radio r y la altura h del cuerpo. Supongamos que tales valores son r = 5.00 ± 0.05 y h = 100.0 ± 0.5. Entonces, el volumen vale V = 7853.9816.... . Para expresar correctamente este resultado hay que determinar cuanto vale su error; así, se calcula el valor de la diferencial de V:
y se sustituyen los diferenciales por errores:
de donde obtenemos que ∆V = 196.34954.... Por tanto, el resultado de la medición del volumen es V = 7900 ± 200.
2) Como ejemplo de aplicación del método de mínimos cuadrados supongamos un experimento en el que se mide el alargamiento de un muelle debido a la acción de una pesa; se trata de comprobar la ley de Hooke. Los datos que se han obtenido son:
Esta tabla puede ser tratada para encontrar las sumatorias oportunas como sigue:
de donde ahora, fácilmente, obtenemos que:
Además se tiene que ∆a = ±0.04 y ∆b = ±2.2
3) Sea la siguiente función
3) Sea la siguiente función
Calcular el polinomio de Taylor de orden 2 de f en Xo = 1 y encontrar la expresión del resto. Con esta estimación, acotar el error que se comete al aproximar f(0,9) por P2(0,9).
Calculemos las derivadas
Para acotar el error, tenemos que
en donde c esta en el intervalo(0,9; 1). Tratemos de acotar
Por un lado, como c < 1 tenemos que
Además 3 + c < 3 + 1 = 4. Entonces,
Por ello,
Con esto vemos que si aproximamos
por
la acotación del resto da
Ejercicios Propuestos
BIBLIOGRAFÍA
[1] Universidad de las Palmas de Gran Canaria. Teoría de errores. [En línea]. Disponible en: https://www2.ulpgc.es/hege/almacen/download/11/11420/teoriaerrores.pdf
[2 ]Torrelavega. Teoría de errores. [En línea]. Disponible en: http://ocw.unican.es/ensenanzas-tecnicas/fisica-i/practicas-1/Teoria%20de%20errores.pdf
[3] Universidad de Málaga. Departamento de física aplicada II. Teoría de Errores. [En línea]. Disponible en: http://webpersonal.uma.es/~JMPEULA/teoria_de_errores.html
[4] Antonio Miguel Posadas Chinchilla. Facultad de Ciencias Experimentales – Universidad de Almería. DETERMINACIÓN DE ERRORES Y TRATAMIENTO DE DATOS. [En línea]. Disponible en: https://w3.ual.es/~aposadas/TeoriaErrores.pdf
[5] Análisis de error y tratamiento de datos obtenidos en el laboratorio. [En línea]. Disponible en: http://airy.ual.es/fisica/seminario.pdf
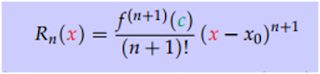
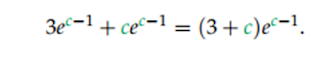
No hay comentarios:
Publicar un comentario